總合
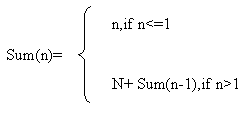
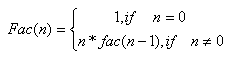
最大公因數
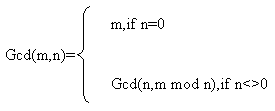
二項係數
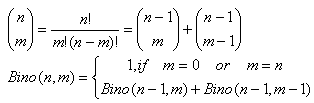
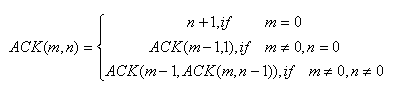
試推導ACK(1,1)=3,ACK(1,2)=4,ACK(2,2)=7等值
費氏級數
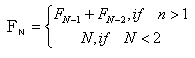
0.概說
分類
程式=演算法+資料結構
資料組織可以區分為:
| 基元資料 (Primitive data) |
字元、整數與實數即位元編碼表示方法 |
| 非基元資料結構 (Non primitive data structure) |
線性Linear 串列List(陣列),堆疊Stack(遞迴),佇列Queue[88保送] 非線性Nonlinear 圖Graph,樹Tree(例如作業系統的樹狀檔案結構) |
此處討論的資料結構,乃是以非基元資料結構為主。
特性
演算法必須符合:(注意:演算法不一定具有正確性!)
演算法的書寫,一般均利用虛擬語言Pseudo-Language書寫,常見有Sparks,Pascal-like語言
效率
程式執行效率的分析,所依據的準則:時間複雜度(所需執行時間),程式大小(所需記憶體空間)以Big-O與Big-Omega為時間複雜度的理論上下限值
意指程序本身具有再呼叫自己的能力。又可分為:
一般而言,如果以if-then-else以及while寫成的程式均可以寫成具有遞迴結構的程式。你可以利用遞迴樹來觀察是否是使用遞迴的時機,如果遞迴樹變的重複動作變多,或是遞迴樹變成一種簡單的形式,便不適合使用遞迴。例如費氏級數的演算,如果利用遞迴,其時間複雜度變成O(2^n/2),而使用非遞迴時,則時間複雜度簡單變為O(n),便是一個很好的例子。
通常可以作遞迴式的有以下範例(不論是否為較佳)
|
總合 |
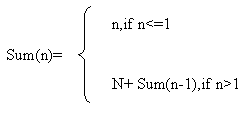 |
| 級數Factorial | 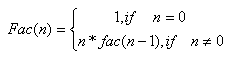 |
|
最大公因數 |
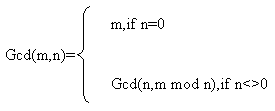 |
|
二項係數 |
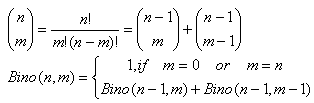 |
| Ackerman級數 |
試推導ACK(1,1)=3,ACK(1,2)=4,ACK(2,2)=7等值 |
|
費氏級數 |
|
2.串列List
串列分為有序串列,與無序串列。有序串列便是指陣列,資料儲存在連續記憶空間;而無序串列則是透過指標Pointer,資料乃是儲存在非連續性的記憶空間,以達成資料的鏈結鏈式串列元素的增減,基本上便是以變更鏈結指標的方式達成,允許資料在串列中的任一位置加入資料,刪除資料等動作。乃是實際需要才配置記憶體本結構的範例以單一鏈結線性串列Singly linked linear list為例,簡要圖形下:
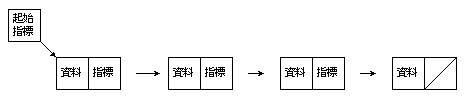
利用變更鏈結指標達成鏈結串列元素的增減,允許在串列中的任何位置進行資料的調整與操作
[程式範例]
資料先進後出的模式LIFO Last in First Out,便是堆疊。例如副程式的呼叫,或是記憶體的使用,便是堆疊的一種應用。 此種資料結構只允許元素在單一位置端增添或刪減。在堆疊中增添資料稱為『推進Push』,刪去元素稱為『移出Pop 』。 此種資料結構利用一個頂端指標,標定堆疊內最頂端的資料位址,當堆疊內的資料變動時,該指標亦同步變動
簡要操作圖形如下: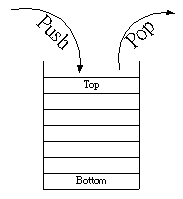 |
疊入程序演算法 PROCEDURE PUSH; if top >=n then full else top =top+1 stack(top)=data endif end |
彈出程序演算法 |
[程式範例]
資料先進先出的模式FIFO First in First out或是FCFSFirst come First service,便是佇列。亦即資料由一端增加,由另一端移出,便屬佇列的應用。如果佇列雙向均可以進出資料,此佇列稱為雙佇列Dequeue:Double Ended Queue操作本資料結構時,首先規劃一段連續的記憶體空間,再利用兩個指標,指向取出元素的一端稱為前端指標Front pointer,指向元素進入的一端為後端指標Rear pointer。元素加入或是刪除,加入或刪除端的指標便指向下一個未使用的記憶體空間(加入時),或是下一個元素的位址(刪除時)。所以經過一段時間後,佇列便有可能超過原先所規劃的記憶體空間,或是必須大幅搬動佇列內的元素,使運算效律變低,導致佇列無法操作。為改善此現象,遂有環狀佇列(Circular queue)的應用。乃指佇列空間的第一個位址與最後一個位址相鄰,除所規劃的記憶體空間被用盡外,此一環狀佇列元素的位址,可被循環使用
簡要操作圖形如右所示: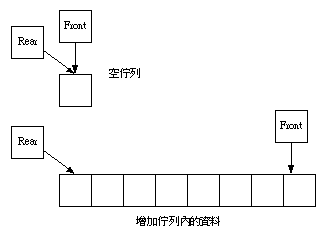
環狀佇列圖形如右: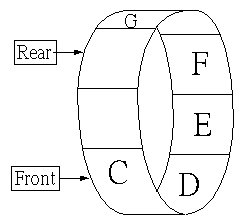
佇列的插入演算法 |
佇列的刪除演算法 |
[程式範例]
樹的結構,一般由最頂端稱為根Root,開始延伸節點node,所延伸出的其他節點稱為支節點Branch Node。在最底端不再延伸的節點稱為終止節點Terminal node 。上下相互兩層節點間的關係可以稱為兄弟節點Twins,而下節點稱為上節點的子節點Children node。常見的資料結構便是計算機組織間的檔案系統或是資料庫結構,均存有樹狀結構的應用,亦即組織層級架構Hierarchic
[程式範例]
所謂排序,乃是指將一組資料依據資料間的特性,或是依據使用者的需求,將資料呈現規則性的序列的一種資料演算方法。基本上資料排序可以分為:
如果排序是比較整個鍵值,則稱為比較排序Comparative sort,否則稱為分配排序distributive sort
對於檔案中的記錄,可能具有相同相同的鍵值,如果兩相同的鍵值在排序前後的位置並未調動,則此排序具有穩定性stable,否則稱為不穩定性排序unstable
排序可以針對記錄本身,或是利用輔助性指標進行。下表是排序法的演算分類與程式範例:
分類 |
種類名稱 |
| 選擇法 | 線性選擇Linear Selection 交換線性選擇Linear Selection with Exchange 計數線性選擇Linear Selection with Counting |
| 插入法 | 線性插入法Linear Insertion 交換法Centered Insertion |
| 交換法 | 氣泡排序法Bubble 成對交換法Pair Exchange 薛爾排序法Shell 快速排序法Quick |
| 樹結構法 | 二元樹法Binary Tree 對抗法Tournament 錐形法Heap |
在Quick Basic中有一則排序的範例程式,請參考
排序法結論
排序法 |
平均時間 |
最差情形 |
穩定度 |
額外空間 |
Selection |
O(n2) |
O(n2) |
不穩定 |
O(1) |
Insertion |
O(n2) |
O(n2) |
穩定 |
O(1) |
Bubble |
O(n2) |
O(n2) |
穩定 |
O(1) |
Shell |
O(n log n) |
O(ns) 1<s<2 |
不穩定 |
O(1) |
Quick |
O(n log n) |
O(n2) |
不穩定 |
O(n log n) O(n) |
Heap |
O(n log n) |
O(n log n) |
不穩定 |
O(1) |
為取得特殊或是指定的資料,而必須掃描一範圍的資料,此掃描的方法便是搜尋。
下表是常見的搜尋法
| 線性搜尋法Linear Search | 不須排序,平均需要搜尋(n+1)/2次 |
| 二元搜尋法Binary Search | 需要排序,可直接讀取檔案。平均需要搜尋log2N次 |
| 插補搜尋法Interpolation Search | 需要排序,可直接讀取檔案 |
| 區域搜尋法Block Search | 大區域須排序,但區域內資料不須排序 |
| 費氏搜尋法Fibonacci Search | 需要排序,可直接讀取檔案 |